OK, I tested my recent changes and the game simulation worked successfully for one of my objectives. The objective would be to have 4 different strategies based on 2 axis:
Buy low sell high VS buy smart: This is the newbie strategy VS the expert strategy.
Concentrated Shares VS Diversified shares: This is the high risk VS low risk strategy.
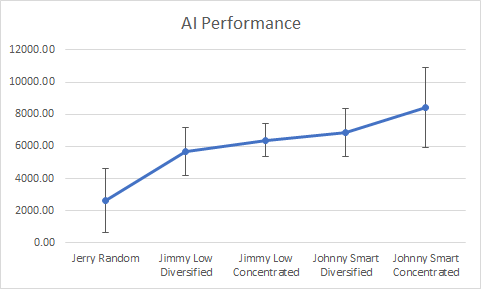
Now I have 5 AI, one for each Strategy plus one doing random actions. Here is the simulation results for 10000 games:
Statistics compilation for each player
Player:Jerry Random 2623.1904
Player:Jimmy Low concentrated 6396.16
Player:Jimmy Low diversified 5695.8193
Player:Johnny Smart concentrated 8434.502
Player:Johnny Smart diversified 6877.638
What is new is that with recent rule changes, the smart AI can now surpass the Buy low AI. So an expert player is rewarded for it's extra efforts.
Now I see that the concentrated AI have better average score than diversified strategies. Does that makes them superior?
The objective is to have high risk, high reward. You can lose a lot, but you can also win a lot. Unless I am mistaken, having more risk would change the distribution on the curve (variant) but the average would remain the same.
Since concentrated AI have an average way higher than diversified strategy, that would be that the game is broken. Concentration is always superior and worth the risk.
I imagine I would need to change additional rules to make sure the concentrated and diversified AI average fortune are equal. Unless there is something I missing. Maybe the psychological effect of playing more risky, will incite players not to do that.
What are your thoughts?






Thanks for the output, you bring interesting points.
Starting money is 500$
Duration is 10 years, composed of 4 turns, so 40 turns. So the value above is average amount of fortune at the end of the 10 year period.
I think that dressing up a curve of the fortune could be something to consider. Maybe some of the players does not have a normal distribution. I could try to distribute the values on a graph.
Comparing winnings and loosings, interesting. I would not be able to put multiple copies of the same AI, at least for the buy low, because the evaluation of the stock (which stock it buy) would always be the same. For the smart AI, I am using Multi Criteria Decision Analysis algorithm, I can give various ponderations that have similar performance, which could lead to players building up different portfolio.